Unlocking Hidden Error Messages in the ExecuteSQL Function
By Daniel Wood, 7 January 2015
EDIT - Simpsons did it!
Well not quite the Simpsons, but maybe you get the cultural reference. Turns out this technique has been referred to previously on the custom function site fmfunctions.com here. Thank you to readers for pointing it out, and Andries Heylen for submitting the function! That is not to say the rest of the article is not interesting, so please carry on reading :)
A Simple ExecuteSQL Query as Illustration
Below we have a very simple query using ExecuteSQl. This query is asking for the field Tasman_URL from a table occurrence named zdev_Settings. This table only has a single record, so we do not require a WHERE clause in the query.
As you can see, when we use the data viewer to evaluate the query, we are given the resulting field value as output, all pretty standard stuff.
Next, lets break the query. To do this we are going to change the field name to Tasman2_URL.
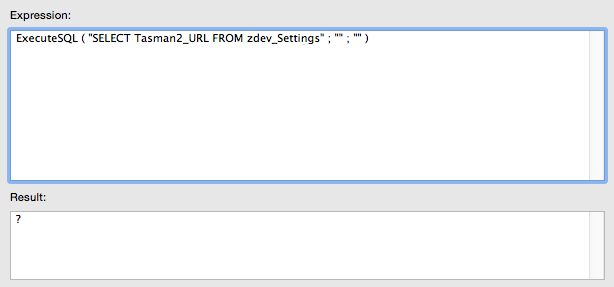
Because this field does not exist, we have a syntax error in the query. Anytime there is an error in our query, FileMaker returns a solitary question mark as output. Oh how useful this is! The question mark tells us something is broken, but most of the time knowing what is broken is hard to track down, particularly in very large queries involving things like joins, where clauses, ordering, aliases etc.
Here's where things get interesting...
So recently I have been developing an internal solution and making more use of ExecuteSQL during development. While testing queries in the data viewer, I happened to enter a particular query in a Let statement. The idea was that if "?" was returned, I wanted the result to be nothing instead of the question mark, eg:
IF ( Query = "?" ; "" ; Query )
When I put this into the data viewer and pressed 'Evaluate' what I saw was quite interesting:
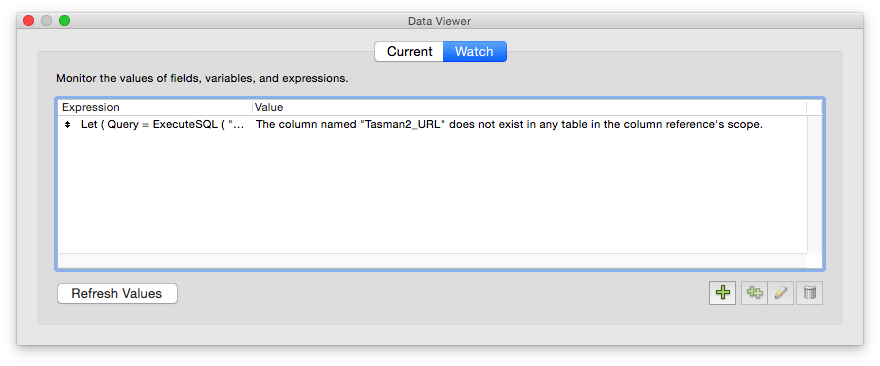
Where did that come from!! The evaluated result of the calculation - which was meant to be nothing - instead was showing as a nice descriptive error message telling me exactly what was wrong in my query.
When I went back into the data viewer calculation, the message was still showing. However as soon as I hit "Evaluate" it disappeared and the expected blank result was shown.
So when does the message appear?
After (not so) extensive testing, I have been able to only reproduce showing the error message in the data viewer, after the "Monitor" button is pressed. Once you go back into the calculation the message remains, but using the "Evaluate" button will cause it to disappear.
The error message does not appear to actually be a result of the calculation, as using the Let statement in scripts and other calculations never yields the message as a result, it appears confined just to the data viewer, which is actually quite a nice place for it to stay.
You can actually get the messages to appear by simply returning blank:
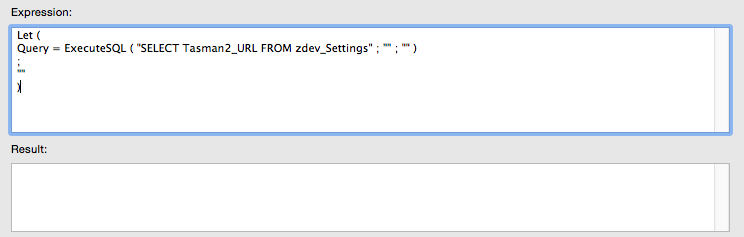
To make good use of it in practice I have created a simple custom function called "SQL" which simply takes the query as input, and outputs blank if the query yields a question mark (otherwise the query result is outputted).
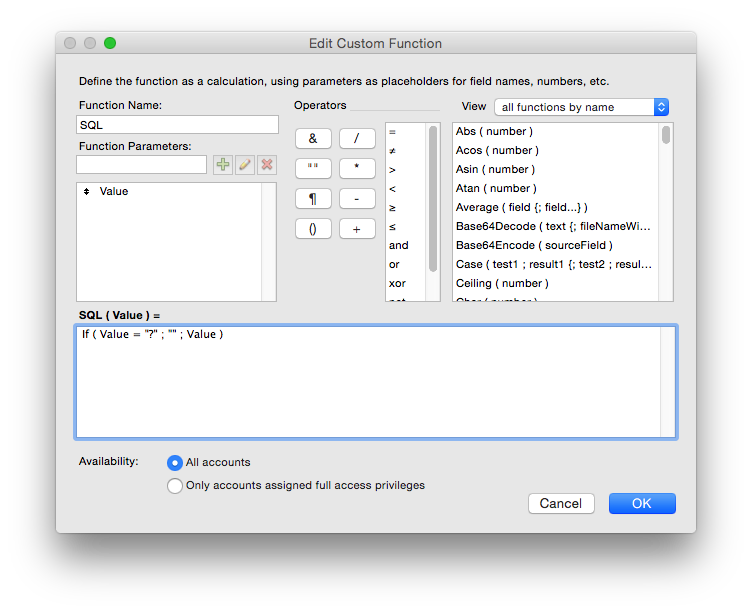
What types of error messages can it return?
Again I have not gone into huge testing here (hopefully the community reading this can do that ;) but I've found a few messages it can return so far. After searching round the internet these may be standard SQL error messages, though not 100% sure on that. Below are three examples of errors produced so far:
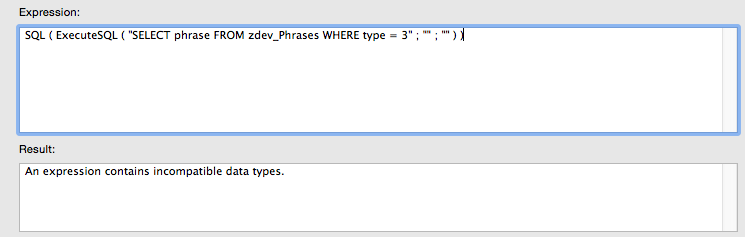
The first one results from an incorrectly named table occurrence. The second is an error in the query syntax - in this case I incorrectly spelt the keyword 'FROM'.
The last example is of a data type mismatch. In this example the field 'type' is a text field, but we are comparing it to a number.
Further testing and discovery
I did some searching round the internet but was unable to find any references to this coming up in the community before. If anyone has come across this peculiarity before I'd be keen to hear it. Also it would be good to know if there is an easier way to extract these messages, and whether they can be obtained by means other than the data viewer. I look forward to hearing peoples results!
Example File
Sorry, I didn't think there was much worth in producing a demo file for this given it is so simply reproduced and FileMaker Pro Advanced is required for the data viewer.
Something to say? Post a comment...
Comments
Daniel Wood 31/07/2018 10:40am (6 years ago)
hi Gazali,
I'm not sure if you are getting executeSQL function in FileMaker confused with SQL in regards to ESS/ODBC integration? The ExecuteSQL function is purely used to query table occurrences in FileMaker (which can be FM/ODBC based). I may need more context from you in relation to your situation in order to help further.
Gazali 23/07/2018 2:40am (6 years ago)
I created select statements with union into a table in FM.
When I run the script , I was asked to create odbc.
I dont have problem with sql. But how do we apply it in filemaker to view results
Jason Lisburn 19/11/2016 2:24pm (8 years ago)
Nice, thanks very much. My case was such that I had some valid 'null' values (some subsections were untitled and therefore no record is kept) and wanted the blank value returned.
Cheers
Eric Chiquet 31/03/2015 12:20am (10 years ago)
Very interesting. I had some question marks when I was using ExecuteSQL function in one of my project. it was not clear enough to know where to find how to solve it. If I can find other error stings I will let you know.
Eric Chiquet
Nick Lightbody 26/01/2015 5:42am (10 years ago)
The SQL error codes are the complete list that FileMaker uses - I am happy to have chat sometime about how to acquire this sort of data.
Cheers, Nick
beverly 25/01/2015 4:58am (10 years ago)
Steve, if you follow my link to the DoSQL2 wiki, they list several errors found by plug-in developers. I don't know where they got them or where Nick got the "list".
Steve Allen 24/01/2015 10:33am (10 years ago)
Nick,
Where did you locate the list of error strings? How can I get the full list?
Steve Allen
Richard Carlton Consulting
DJ 09/01/2015 6:52pm (10 years ago)
I'm going to follow the comments...
Nick Lightbody 09/01/2015 12:11pm (10 years ago)
Maybe it is just experimental - not QAed - not approved - just under development - waiting for enough market pressure for it to be finished and announced?
Bev - thanks for the clarification.
Cheers, Nick
Daniel Wood 09/01/2015 9:45am (10 years ago)
I wonder also why this type of thing is not documented with FM or an actual feature not hidden away. Imagine a new parameter to executeSQL for debugging, such that when used it returns the error message (although FM would never have that type of 'flag' parameter to a function) - perhaps just using EvaluationError and returning the message would be useful. Or even better yet, the calc engine should be able to recognize the first parameter to the function is always going to be an SQL query, so it would be nice if it could auto-format it for you, eg adding in double quotes or single quotes where required, highlighting errors in red etc (one day maybe!)
beverly 09/01/2015 4:57am (10 years ago)
sorry, the post got munged - the wiki link is here
http://wiki.myfmbutler.com/index.php/DoSQL_2#Errors_returned_by_DoSQL
beverly 09/01/2015 4:53am (10 years ago)
I got the information on the 8309 and 8310 error codes from the FM Plug-ins for SQL. Specifically, you can check the "myFMbutler DoSQL plug-in Release Notes" or the wiki <http://wiki.myfmbutler.com/index.php/DoSQL_2#Errors_returned_by_DoSQL>, but I believe all the SQL plug-in developers test for them.
When I got one of these errors, first I checked for my own mis-typing. Then I just tested the heck out of variations of the query. That's what led to my reference (http://filemakerhacks.com/2012/11/02/pdf-version-of-the-missing-fm-12-executesql-reference/>.
Yes, I think these error codes should be listed in the FM documentation. :)
Nick Lightbody 09/01/2015 3:14am (10 years ago)
Hi Jonathan, sorry but I am not sure where the error codes from Bev's suggestion come from / where they are documented?
They are not normal FM codes which only go up to 1507 under FM13.
I generated "8309" by misnaming a table occurrence in my SQL expression - the FQL message was "The table named "xUi" does not exist." Monkeybread have a ref to Filemaker Error 8309 but this seems to be for a different event.
I think we need Bev to tell us where to find these codes?
However - perhaps we don't need them as the FQL messages are clearly designed to specifically meet the needs of someone developing using the FQL?
I have tried various error states and whilst the messages reflect the first error they parse - of several for example - the Error Code doesn't appear to change - in my tests it was either 0 or 8309.
Cheers, Nick
Jonathan Fletcher 09/01/2015 2:23am (10 years ago)
Thanks, Nick! Hey, do you have a list with the error codes, so they can be used with the function that Beverly mentioned?
Daniel Wood 09/01/2015 12:06am (10 years ago)
Cheers Nick, I'll grab them off the linkedin comment and add them to the article, thanks again!
Nick Lightbody 08/01/2015 11:30pm (10 years ago)
No sure that the full list appears in my comment above - give me your email address Daniel and I will send you the full list - there are 52 rows - I have added them as a comment to your LinkedIn item
Nick
Nick Lightbody 08/01/2015 11:21pm (10 years ago)
Daniel - thank you very helpful and thank you also to to Bev for the EvaluationError() approach - a quick search didn't find a specific SQL error code table to match the errors I was getting.
As a general reference I have added below the FileMaker 13 error messages that Daniel's technique should reveal - they are what FMI call FQL (I assume Filemaker Query Language) strings.
Cheers, Nick
FQL Strings: FMA13v4:
There is an error in the syntax of the query.
The table named "0" does not exist.
The table named "0" already exists in this query.
The query is too complex. The maximum number of tables has been exceeded.
Expressions involving aggregations are not supported.
The column named "0" appears in more than one table in the column reference's scope.
The column named "0" does not exist in any table in the column reference's scope.
The table named "0" does not exist in the column reference's scope.
The column named "1" does not exist in table "0".
The literal value "0" is not a valid DATE, TIME or TIMESTAMP.
Predicate must contain a logical operation (=, <, OR, AND, IS NULL, ...).
The ordinal reference "0" in the ORDER BY clause is not valid.
Incompatible types in assignment.
The number of values in a VALUES row value constructor does not match the number of values in the target.
The number of values in an INSERT...SELECT statement does not match the number of values in the target.
A subquery contains an illegal outer reference to a column in the INSERT's target table.
An expression contains data types that cannot be compared.
An expression contains incompatible data types.
The result data type of a CASE expression cannot be inferred; they are all NULL.
An invalid number of parameters was supplied to the function "0"
Parameter number 0 to the function "1" is not of the correct type.
A subquery expression must have exactly one value in the SELECT list.
A CAST expression requested an invalid data type conversion.
A reference to ROWID must be qualified if more than one table is present in the query.
All non-aggregated column references in the SELECT list and HAVING clause must be in the GROUP BY clause.
The number of columns in both inputs to a UNION operation must be the same.
The data types of corresponding columns in the inputs to a UNION operation must be the same.
Field repetitions must be numeric and between 1 and 0.
A field repetition in the SET clause of an UPDATE statement must be a constant.
"0" is an invalid function.
The the parameter's type cannot be inferred in this context. At least one query parameter must be an expression, a column or a constant.
A query may contain either named parameters or dynamic parameters, but not both.
Column names in FROM clause subqueries must be unique.
The number of output columns in a FROM clause subquery must match the number of columns in the table's name list.
Cursor support is not enabled for this query.
A cursor with the name "0" already exists.
There is no cursor with the name "0".
The cursor "0" is already open.
The cursor "0" is not open.
The target cursor "0" does not reference a query that is valid for WHERE CURRENT OF <cursor>.
The target cursor "0" does not reference the same table as the current statement.
The default value for column "0" does not match the column's data type.
The string "0" is not a valid stream name.
The column "0" is not valid in this context. The targets of GETAS and PUTAS must be Container fields.
The value 0 is not a valid binary string.
Container fields are not allowed in UNION DISTINCT queries.
The database schema has changed. This prepared query is no longer valid.
This statement contains an invalid operation on FileMaker system table "0".
Aggregation expressions are not allowed in the WHERE clause.
The offset count in OFFSET clause is not valid.
The FETCH ... WITH TIES clause is not allowed without a corresponding ORDER BY clause.
The fetch count in FETCH clause is not valid.
[ENDS]
Fabio 08/01/2015 9:53am (10 years ago)
Amazing! Very useful in dev.
Thank you, Daniel :)
Beverly, too!
Jonathan Fletcher 08/01/2015 9:18am (10 years ago)
Thankyouthankyouthankyou!
beverly 08/01/2015 4:50am (10 years ago)
And the EvaluationError() function will give you the CODE for the error (if you want to look them up).
Daniel Wood 07/01/2015 10:17pm (10 years ago)
Hi guys, thanks for the comments. Chris turns out you were correct, as some readers on linkedin and facebook mentioned, a developer did discover this a couple of years back and put a custom function up on fmfunctions.com. I have ammended the start of the article to give info on this, cheers!
Chris Van Buren 07/01/2015 9:24pm (10 years ago)
Thanks for the discovery and proper write up of it. I think I was aware of a similar thing that I had seen somewhere but can't pin it down. Still this is a great contribution. I'll let you know if I am able to track down my earlier reference but Spotlight and Google are failing me...
Damon Casey 07/01/2015 8:41pm (10 years ago)
Interesting find, Daniel. How many more undocumented features can there be?
No one has commented on this page yet.
RSS feed for comments on this page | RSS feed for all comments